Glossari
Aquest glossari és una mostra dels termes més representatius de Karl Weierstrass. Les definicions han estat extretes dels recursos següents:
Wikipedia en anglès (WIKIPEDIA-EN)
Wikipedia en castellà (WIKIPEDIA-ES)
Wolfram Science (WOLFRAM)
Bolzano-Weierstrass theorem
In mathematics, specifically in real analysis, the Bolzano–Weierstrass theorem, named after Bernard Bolzano and Karl Weierstrass, is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states that each bounded sequence in Rn has a convergent subsequence. An equivalent formulation is that a subset of Rn is sequentially compact if and only if it is closed and bounded. The theorem is sometimes called the sequential compactness theorem.
Citació: "Bolzano–Weierstrass theorem" A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://en.wikipedia.org/wiki/Bolzano%E2%80%93Weierstrass_theorem>
Més informació:
WolframCalculus of variations
El cálculo de variaciones es un problema matemático consistente en buscar máximos y mínimos (o más generalmente extremos relativos) de funcionales continuos definidos sobre algún espacio funcional. Constituyen una generalización del cálculo elemental de máximos y mínimos de funciones reales de una variable
Citació: "Cálculo de variaciones" A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/C%C3%A1lculo_de_variaciones>
Més informació:
WolframCasorati–Weierstrass theorem
In complex analysis, a branch of mathematics, the Casorati–Weierstrass theorem describes the behaviour of holomorphic functions near their essential singularities. It is named for Karl Theodor Wilhelm Weierstrass and Felice Casorati. In Russian literature it is called Sokhotski's theorem.
Citació: "Casorati-Weierstrass" A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://en.wikipedia.org/wiki/Casorati%E2%80%93Weierstrass_theorem>
Més informació:
WolframComplex analysis
El análisis complejo (o teoría de las funciones de variable compleja) es la rama de las matemáticas que en parte investiga las funciones holomorfas, también llamadas funciones analíticas. Una función es holomorfa en una región abierta del plano complejo si está definida en esta región, toma valores complejos y por último es diferenciable en cada punto de esta región abierta con derivadas continuas.
Citació: "Análisis complejo". A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/An%C3%A1lisis_complejo>
Més informació:
Lindemann–Weierstrass theorem
El teorema de Lindemann–Weierstrass es un resultado muy útil para establecer la trascendencia de un número. Afirma que si α1, α2, ...,αn son números algebraicos linealmente independientes sobre el cuerpo de los números racionales 
, entonces 
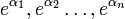son algebraicamente independientes sobre ; es decir, el grado de trascendencia de la extensión del cuerpo 
sobre es n.
Lindemann demostró en 1882 que eα es trascendente para todo α algebraico no nulo, y de este modo estableció que π es transcendente. Weierstrass demostró la forma más general de este teorema en 1885.
El teorema anterior junto con el Teorema de Gelfond-Schneider, está generalizado por conjetura de Schanuel.
Citació: "Teorema de Lindemann–Weierstrass". A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/Teorema_de_Lindemann%E2%80%93Weierstrass>
Més informació:
Real analysis
El análisis real o teoría de las funciones de variable real es la rama del análisis matemático que tiene que ver con el conjunto de los números reales. En particular, estudia las propiedades analíticas de las funciones y sucesiones de números reales; su límite, continuidad y el cálculo de los números reales.
Citació: "Análisis real". A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/An%C3%A1lisis_real>
Més informació:
WolframStone-Weierstrass theorem
En análisis matemático, el teorema de aproximación de Weierstrass es un resultado que afirma que las funciones reales continuas definidas en un intervalo cerrado y acotado pueden ser aproximadas tanto como se quiera por un polinomio. Es decir, los polinomios de coeficientes reales son densos en el conjunto de las funciones continuas sobre un intervalo cerrado.
Karl Weierstrass dio una demostración de este resultado en 1885. Posteriormente, Marshall H. Stone generalizó el teorema (Stone, 1937) y simplificó la demostración. A esta generalización se la conoce como el teorema de Stone–Weierstrass.
Citació: "Teorema de aproximación de Weierstrass". A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/Teorema_de_aproximación_de_Weierstrass>
Més informació:
WolframUniform continuity
En análisis matemático una función f(x) se dice que es uniformemente continua si pequeños cambios en el valor de x producen pequeños cambios en el valor de la función (continuidad) y el tamaño de los cambios en f(x) depende solo del tamaño de los cambios en x pero no del valor de x (uniforme).
Citació: "Continuidad uniforme" A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/Continuidad_uniforme>
Més informació:
Uniform convergence
In the mathematical field of analysis, uniform convergence is a type of convergence stronger than pointwise convergence. A sequence {fn} of functions converges uniformly to a limiting function f if the speed of convergence of fn(x) to f(x) does not depend on x.
The concept is important because several properties of the functions fn, such as continuity and Riemann integrability, are transferred to the limit f if the convergence is uniform.
Weierstrass function
La función de Weierstrass es muy particular. Su nombre, por supuesto es por su mentor, quien la publicó por primera vez, Karl Weierstrass. Está definida en la recta y toma valores reales. Lo que la hace particular es que es continua en todo punto y no es derivable o diferenciable en ninguno. Además resulta que el grafo de la función de Weierstrass es una curva no rectificable de dimensión fractal superior a 1.
Citació: "Función de Weierstrass" A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/Funci%C3%B3n_de_Weierstrass>
Més informació:
Weierstrass p function
En el ámbito de las matemáticas, las funciones elípticas de Weierstrass son un grupo de funciones elípticas que poseen una forma particularmente simple (cf funciones elípticas de Jacobi); han sido designadas en honor al matemático Karl Weierstrass. Esta clase de funciones es también llamada funciones P y generalmente se las escribe utilizando el símbolo 
(que corresponde a una letra P estilizada, llamada P de Weierstrass)
Citació: "Funciones elípticas de Weierstrass" A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/Funciones_el%C3%ADpticas_de_Weierstrass>
Més informació:
Wikipedia en
Weierstrass theorem
El Teorema de Weierstrass es un teorema de análisis real que establece que una función continua en un intervalo cerrado y acotado (de números reales) alcanza sus valores máximo y mínimo en puntos del intervalo. También se puede enunciar en términos de conjuntos compactos. El teorema establece que una función continua transforma intervalos conexos en intervalos compactos, entendiéndose por intervalo compacto aquel que es cerrado (sus puntos frontera le pertenecen) y acotado.
Citació: "Teorema de Weierstrass". A Wikipedia. Wikimedia Foundation, 2011. 30 setembre 2014. <http://es.wikipedia.org/wiki/Teorema_de_Weierstrass>
Més informació:
Comparteix: